Любой специалист, работающий с электроникой, будь то радиолюбитель-энтузиаст или профессиональный инженер-схемотехник, рано или поздно сталкивается с необходимостью расчета параметров цепей, содержащих несколько индуктивных элементов. Если вычисление индуктивности одиночного соленоида является относительно тривиальной задачей, то появление в схеме второй катушки вносит существенные коррективы в привычные формулы. Взаимодействие их магнитных полей порождает явление, которое нельзя игнорировать для получения точных результатов. Для создания таких схем часто требуются качественные радиоэлектронные компоненты, широкий выбор которых представлен на ресурсе https://radaelectron.ru, но перед покупкой и применением важно досконально разобраться в теоретической базе. Эта статья станет вашим подробным путеводителем в мир расчета индуктивности связанных катушек, объясняя все нюансы от базовых понятий до практических методов измерения.
Что такое индуктивность и почему она важна?
Прежде чем погружаться в сложности взаимодействия двух катушек, необходимо четко понимать, что представляет собой индуктивность как физическое явление. Говоря простыми словами, индуктивность — это свойство проводника (чаще всего выполненного в виде катушки) накапливать энергию в магнитном поле при протекании через него электрического тока. Она проявляется как способность противодействовать любым изменениям этого тока. Это своего рода электрическая инерция: подобно тому, как массивное тело не может мгновенно изменить свою скорость, катушка индуктивности не позволяет току в цепи измениться скачкообразно.
Измеряется индуктивность в Генри (Гн), названных в честь американского ученого Джозефа Генри. На практике один Генри — это очень большая величина, поэтому в радиоэлектронике чаще всего оперируют дольными единицами:
- Миллигенри (мГн), равный 10-3 Гн.
- Микрогенри (мкГн), равный 10-6 Гн.
- Наногенри (нГн), равный 10-9 Гн.
Это свойство является краеугольным камнем для огромного числа электронных устройств. Без катушек индуктивности были бы невозможны трансформаторы, электродвигатели, реле, колебательные контуры в радиоприемниках и передатчиках, а также высокоэффективные импульсные источники питания.
Индуктивность — это фундаментальное свойство, которое лежит в основе работы трансформаторов, двигателей, фильтров и множества других электронных устройств. Понимание ее природы — ключ к успешному проектированию и ремонту электроники.
Переход от одной катушки к двум: введение в понятие взаимной индуктивности
Когда в пространстве находится только одна катушка, ее индуктивность зависит исключительно от ее собственных геометрических и физических параметров. Однако ситуация кардинально меняется при появлении второй катушки. Любой проводник с током создает вокруг себя магнитное поле. Если вторая катушка попадает в это поле, то переменный магнитный поток, создаваемый первой катушкой, будет пронизывать витки второй, индуцируя в ней электродвижущую силу (ЭДС). Этот процесс является двусторонним. Так возникает явление электромагнитной индукции между двумя отдельными цепями, которое характеризуется параметром под названием взаимная индуктивность (или коэффициент взаимной индукции).
Рис. 1. Взаимодействие магнитных полей двух соседних катушек — основа явления взаимной индуктивности.
Взаимная индуктивность, обозначаемая буквой M и также измеряемая в Генри, показывает, насколько эффективно магнитное поле одной катушки связано с другой. Именно этот параметр становится ключевым дополнением в формулах расчета общей индуктивности системы из двух катушек.
Взаимная индуктивность (M) — это мера магнитной связи между двух катушек, и ее учет является обязательным для правильного расчета общей индуктивности цепи.
Основные формулы расчета: согласное и встречное включение
Когда две катушки соединены последовательно, их общая индуктивность зависит не только от их индивидуальных значений L1 и L2, но и от взаимной индуктивности M, а также от способа их подключения. Существует два фундаментальных способа соединения, которые дают кардинально разные результаты.
1. согласное включение (series-aiding)
Согласным называется такое последовательное соединение, при котором магнитные потоки, создаваемые обеими катушками, направлены в одну сторону и, как следствие, складываются. Это приводит к увеличению суммарного магнитного поля и, соответственно, к максимальной итоговой индуктивности. Представьте, что вы наматываете вторую катушку как продолжение первой, сохраняя то же направление намотки. Визуально на схемах начало обмоток часто помечают точками. При согласном включении ток входит в «точку» первой катушки и в «точку» второй (или, наоборот, выходит из обеих «точек»).
Формула для расчета общей индуктивности при согласном включении выглядит следующим образом:
Lобщ = L1 + L2 + 2M
Где:
- Lобщ — общая индуктивность системы, Гн.
- L1 — индуктивность первой катушки, Гн.
- L2 — индуктивность второй катушки, Гн.
- M — их взаимная индуктивность, Гн.
2. встречное включение (series-opposing)
При встречном включении катушки соединяются так, что их магнитные потоки направлены навстречу друг другу. В результате они взаимно ослабляются, что ведет к уменьшению суммарного магнитного поля. Итоговая индуктивность в этом случае будет минимальной. На схемах это соответствует ситуации, когда ток входит в «точку» одной катушки, а выходит из «точки» другой.
Формула для расчета общей индуктивности при встречном включении:
Lобщ = L1 + L2 — 2M
Правильное определение типа соединения — согласного или встречного — является первым и самым важным шагом в расчете. Ошибка на этом этапе приведет к абсолютно неверному результату.
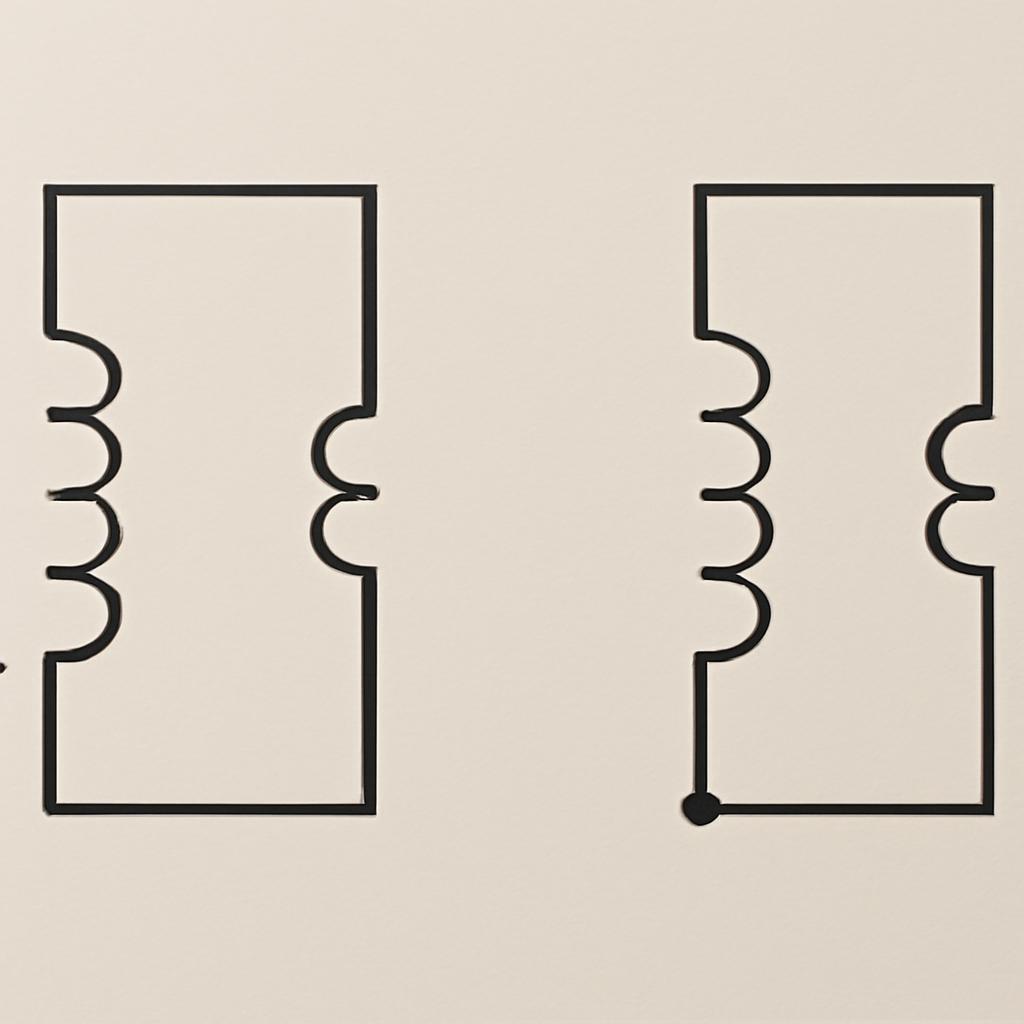
Рис. 2. Схематичное различие между согласным (слева) и встречным (справа) включением. Точки указывают на начало обмоток.
Коэффициент связи (k) — ключ к определению m
Мы видим, что в обеих формулах присутствует взаимная индуктивность M. Но как ее найти? Напрямую измерить M бывает затруднительно. Однако ее можно легко рассчитать, зная индуктивности L1, L2 и так называемый коэффициент магнитной связи (k). Этот безразмерный коэффициент показывает, какая доля магнитного потока одной катушки пронизывает витки другой. Он может принимать значения от 0 до 1.
- k = 0: Связь отсутствует. Катушки находятся очень далеко друг от друга, или их оси перпендикулярны. Магнитное поле одной никак не влияет на другую. В этом случае M = 0.
- 0 Частичная связь. Это наиболее распространенный случай в реальных устройствах. Чем ближе катушки и чем более соосно они расположены, тем ближе k к единице.
- k = 1: Идеальная или полная связь. Весь магнитный поток от первой катушки пронизывает вторую. Это идеализированная модель, к которой стремятся в силовых трансформаторах, наматывая обмотки на общий замкнутый магнитопровод.
Зная коэффициент связи, взаимную индуктивность можно найти по формуле:
M = k * √(L1 * L2)
Коэффициент связи ‘k’ — это безразмерная величина, которая на практике говорит нам, насколько ‘хорошо’ две катушки ‘слышат’ друг друга в электромагнитном смысле.
Таким образом, наши формулы для общей индуктивности принимают более практический вид:
Для согласного включения: Lобщ = L1 + L2 + 2k√(L1 * L2)
Для встречного включения: Lобщ = L1 + L2 — 2k√(L1 * L2)
Сравнительная таблица методов включения
Для наглядности сведем ключевые различия между двумя типами соединений в таблицу.
| Параметр | Согласное включение | Встречное включение |
|---|---|---|
| Взаимодействие магнитных полей | Поля складываются, усиливая друг друга | Поля вычитаются, ослабляя друг друга |
| Итоговая индуктивность (Lобщ) | Максимально возможная (L1 + L2 + 2M) | Минимально возможная (L1 + L2 — 2M) |
| Энергия магнитного поля | Максимальная | Минимальная |
| Типичное применение | Сложение индуктивностей, обмотки трансформаторов для повышения напряжения | Дифференциальные дроссели, компенсационные обмотки, создание неиндуктивных соединений |
Типичные значения коэффициента связи в различных устройствах
Коэффициент связи напрямую зависит от конструкции и назначения узла. Понимание его примерных значений для разных типов устройств помогает в предварительных расчетах и диагностике.
Рис. 3. Примерное распределение силы магнитной связи в популярных радиоэлектронных устройствах.
Как видно из диаграммы, в высокочастотных колебательных контурах часто требуется слабая связь (k 1) для минимизации потерь энергии.
Выбор конструкции (тип сердечника, расположение обмоток) напрямую определяет коэффициент связи, а следовательно, и рабочие характеристики всего устройства, будь то фильтр или источник питания.
Практический метод определения взаимной индуктивности и коэффициента связи
Теоретические формулы прекрасны, но в реальной жизни мы редко знаем коэффициент связи ‘k’ заранее. Чаще всего перед инженером или радиолюбителем стоит обратная задача: имея две катушки, определить их взаимную индуктивность M и коэффициент связи k, чтобы затем использовать эти данные в расчетах. К счастью, существует элегантный и очень точный экспериментальный метод, основанный на тех же самых формулах согласного и встречного включения.
Суть метода заключается в проведении двух измерений общей индуктивности при двух разных способах последовательного соединения катушек. Для этого нам понадобится измерительный прибор — LCR-метр. Это специализированный прибор, предназначенный для измерения индуктивности (L), емкости (C) и сопротивления (R), который является основным рабочим инструментом при работе с индуктивными компонентами.
Алгоритм экспериментального определения m и k
Процедура состоит из нескольких простых шагов, которые позволяют, зная только значения измеренных индуктивностей, вычислить все недостающие параметры. Вот пошаговая инструкция:
- Измерение индивидуальных индуктивностей. Первым делом необходимо измерить индуктивность каждой катушки по отдельности. Убедитесь, что вторая катушка находится на значительном расстоянии, чтобы ее магнитное поле не влияло на измерение. Запишите полученные значения как L1 и L2.
- Измерение при согласном включении (Lсогл). Соедините катушки последовательно. Как определить, что включение согласное, если нет маркировки? Очень просто: сначала соедините их произвольно и измерьте общую индуктивность. Затем, не разрывая цепь, поменяйте местами выводы только одной из катушек и проведите измерение снова. Большее из двух полученных значений и будет индуктивностью при согласном включении, Lсогл. Запишите его.
- Измерение при встречном включении (Lвстр). Меньшее из двух значений, полученных на предыдущем шаге, будет соответствовать индуктивности при встречном включении, Lвстр. Запишите это значение.
- Вычисление взаимной индуктивности (M). Теперь у нас есть все данные для расчета M. Вспомним наши основные формулы:
Lсогл = L1 + L2 + 2M
Lвстр = L1 + L2 — 2M
Если вычесть второе уравнение из первого, мы получим: Lсогл — Lвстр = (L1 + L2 + 2M) — (L1 + L2 — 2M) = 4M
Отсюда легко выражается взаимная индуктивность:M = (Lсогл — Lвстр) / 4
- Вычисление коэффициента связи (k). После того как мы нашли M, рассчитать коэффициент связи ‘k’ не составляет труда, используя измеренные ранее L1 и L2:
k = M / √(L1 * L2)
Подставив выражение для M из предыдущего шага, получим универсальную формулу для ‘k’, выраженную только через измеренные общие индуктивности:
k = (Lсогл — Lвстр) / (4 * √(L1 * L2))
Практический совет: Если у вас нет маркировки начала обмоток, самый надежный способ найти согласное и встречное включение — это выполнить два измерения, поменяв полярность одной из катушек. Большее значение всегда соответствует согласному включению, а меньшее — встречному.
Пример практического расчета
Давайте закрепим теорию на конкретном примере. Предположим, у нас есть две катушки без сердечника, расположенные рядом. Мы хотим узнать их взаимную индуктивность и коэффициент связи.
- Берем LCR-метр и измеряем индуктивность первой катушки: L1 = 50 мкГн.
- Измеряем индуктивность второй катушки: L2 = 80 мкГн.
- Соединяем их последовательно и измеряем общую индуктивность. Получаем 145 мкГн.
- Меняем местами выводы второй катушки и проводим измерение снова. Теперь прибор показывает 115 мкГн.
Итак, мы определили, что:
- Lсогл = 145 мкГн
- Lвстр = 115 мкГн
Теперь применим наши формулы:
1. Находим взаимную индуктивность M:
M = (145 мкГн — 115 мкГн) / 4 = 30 мкГн / 4 = 7.5 мкГн.
2. Находим коэффициент связи k:
k = M / √(L1 * L2) = 7.5 / √(50 * 80) = 7.5 / √(4000) ≈ 7.5 / 63.25 ≈ 0.118.
Наш расчет показывает, что катушки имеют довольно слабую связь (k ≈ 0.12 или 12%), что типично для воздушных катушек, расположенных на некотором расстоянии друг от друга. Теперь, зная эти параметры, мы можем с уверенностью использовать данные катушки в своих схемах, точно предсказывая их поведение.
Что делать, если нет LCR-метра?
Хотя LCR-метр является предпочтительным инструментом, его отсутствие — не приговор. Индуктивность можно измерить и косвенными методами. Один из самых популярных — метод резонанса. Для этого понадобится генератор сигналов (ГСС) и осциллограф (или вольтметр переменного тока).
Суть метода: исследуемая катушка (или система из двух катушек) подключается параллельно с конденсатором известной и точной емкости (C), образуя колебательный контур. На этот контур подается сигнал с генератора. Плавно изменяя частоту генератора, мы с помощью осциллографа ищем частоту (fрез), на которой напряжение на контуре будет максимальным. Это и есть резонансная частота. Зная ее и емкость конденсатора, индуктивность можно рассчитать по формуле Томсона:
L = 1 / ((2πfрез)2 * C)
Проведя эту процедуру для L1, L2, Lсогл и Lвстр, можно получить все исходные данные для дальнейших расчетов по описанному выше алгоритму. Этот метод более трудоемок и требует дополнительного оборудования, но дает вполне приемлемые результаты для многих радиолюбительских задач.
Факторы, влияющие на взаимную индуктивность и коэффициент связи
Понимание формул и методов измерения — это половина дела. Для грамотного проектирования электронных схем необходимо четко представлять, какие физические факторы определяют величину взаимной индуктивности (M) и коэффициента связи (k). Умение управлять этими параметрами позволяет целенаправленно создавать как системы с максимально жесткой связью (трансформаторы), так и развязанные цепи, где взаимное влияние сведено к минимуму (для борьбы с паразитными наводками).
Ключевых факторов, от которых зависит сила магнитной связи, несколько. Рассмотрим каждый из них подробнее.
1. расстояние между катушками
Это самый очевидный и интуитивно понятный фактор. Напряженность магнитного поля убывает с расстоянием от источника. Следовательно, чем дальше катушки расположены друг от друга, тем меньшая часть магнитного потока от первой катушки достигает второй. Связь ослабевает, и значения M и k стремятся к нулю. Эта зависимость нелинейная; даже небольшое увеличение расстояния между близко расположенными катушками может привести к значительному падению коэффициента связи. Именно поэтому в компактных устройствах взаимное расположение индуктивных компонентов на печатной плате играет критически важную роль.
2. взаимная ориентация осей катушек
Расположение катушек в пространстве относительно друг друга не менее важно, чем расстояние между ними. Здесь можно выделить три основных случая:
- Соосное расположение (оси совпадают). Когда катушки намотаны на одном каркасе или расположены на одной оси, одна за другой, магнитная связь будет максимальной для данного расстояния. Почти все силовые линии, выходящие из торца одной катушки, входят в торец другой.
- Параллельное расположение (оси параллельны). Если катушки лежат рядом, их оси параллельны. Связь в этом случае будет слабее, чем при соосном расположении, так как значительная часть магнитного потока рассеивается в пространстве и не пересекает витки соседней катушки.
- Перпендикулярное расположение (оси перпендикулярны). В идеальном случае, когда ось одной катушки перпендикулярна плоскости витков другой, их взаимная индуктивность равна нулю (k=0). Магнитный поток одной катушки проходит параллельно виткам другой и не индуцирует в ней ЭДС. Этот принцип широко используется в радиоаппаратуре для минимизации нежелательных связей между контурами и каскадами.
3. наличие и материал магнитопровода (сердечника)
Материал, находящийся внутри и вокруг катушек, оказывает колоссальное влияние на индуктивность. Сердечник из ферромагнитного материала (например, феррита или электротехнической стали) обладает способностью «концентрировать» в себе линии магнитного поля.
Если обе катушки размещены на общем сердечнике, особенно замкнутой формы (тороидальный, Ш-образный), то этот сердечник становится общим путем для их магнитных потоков. Он буквально заставляет почти весь поток, созданный одной обмоткой, пройти через вторую. Это приводит к резкому увеличению взаимной индуктивности M и приближению коэффициента связи k к единице. Именно на этом принципе основана работа всех силовых и согласующих трансформаторов.
Катушки без сердечника («воздушные») имеют значительно более низкий коэффициент связи, так как их магнитное поле свободно рассеивается в окружающем пространстве.
| Конфигурация катушек | Ориентировочный коэффициент связи (k) | Типичное применение |
|---|---|---|
| Две обмотки на общем тороидальном ферритовом сердечнике | 0.98 – 0.998 | Силовые трансформаторы, импульсные источники питания, широкополосные ВЧ трансформаторы |
| Две обмотки на Ш-образном сердечнике с зазором | 0.95 – 0.98 | Обратноходовые преобразователи, дроссели накопления энергии |
| Две соосные катушки на одном «воздушном» каркасе | 0.2 – 0.6 | Полосовые фильтры, контуры ПЧ в радиоприемниках |
| Две катушки рядом на печатной плате (оси параллельны) | 0.05 – 0.2 | Слабосвязанные контуры, непреднамеренная паразитная связь |
| Две катушки с взаимно перпендикулярными осями | Развязка каскадов, минимизация перекрестных помех (crosstalk) |
4. экранирование
Для минимизации нежелательной связи одну или обе катушки можно поместить в металлический экран (обычно из алюминия или меди). По принципу электромагнитной индукции переменное магнитное поле катушки наводит в экране вихревые токи (токи Фуко). Эти токи, в свою очередь, создают собственное магнитное поле, направленное навстречу исходному полю и компенсирующее его за пределами экрана. Экранирование является эффективным способом изоляции индуктивных компонентов друг от друга, но стоит помнить, что оно также несколько снижает собственную индуктивность и добротность катушки.
Совет эксперта: При проектировании печатных плат для минимизации паразитных связей между катушками индуктивности или дросселями располагайте их так, чтобы их оси были взаимно перпендикулярны. Это простой и бесплатный способ значительно улучшить электромагнитную совместимость устройства.
Таким образом, расчет индуктивности двух катушек — это не просто подстановка чисел в формулу. Это процесс, требующий понимания физики взаимодействия магнитных полей и учета конструктивных особенностей электронного узла. Правильно оценив и управляя расстоянием, ориентацией и использованием сердечников, можно добиться желаемых характеристик схемы, будь то максимальная передача энергии в трансформаторе или, наоборот, полная электромагнитная развязка чувствительных каскадов.
Практическое применение и типичные ошибки при расчетах
Теория и практика расчета индуктивности связанных катушек находят широкое применение в самых разнообразных областях электроники. Понимание этих принципов позволяет не только создавать новые устройства, но и эффективно диагностировать и ремонтировать существующие. Давайте рассмотрим, где эти знания необходимы, и какие подводные камни могут встретиться на пути.
Где используются связанные индуктивности?
Системы из двух и более магнитно-связанных катушек являются основой для множества ключевых компонентов:
- Трансформаторы. Это самое очевидное и распространенное применение. В силовых, звуковых или импульсных трансформаторах две (или более) обмотки намотаны на общий сердечник для достижения максимального коэффициента связи (k → 1). Расчеты, учитывающие взаимную индуктивность, необходимы для определения коэффициента трансформации, согласования импедансов и анализа потерь.
- Полосовые фильтры и колебательные контуры. В радиоприемной и передающей аппаратуре часто используются связанные контуры для формирования нужной амплитудно-частотной характеристики (АЧХ). Регулируя расстояние между катушками (и, следовательно, коэффициент связи k), можно изменять полосу пропускания фильтра, делая ее более узкой или широкой.
- Беспроводная передача энергии (WPT). Современные технологии беспроводной зарядки для смартфонов, электромобилей и медицинских имплантов основаны на принципе магнитно-резонансной связи. Катушка-передатчик и катушка-приемник образуют систему со слабой или средней связью. Точный расчет взаимной индуктивности здесь критически важен для достижения максимального КПД передачи энергии на заданном расстоянии.
- Датчики приближения и металлодетекторы. Работа многих индуктивных датчиков основана на изменении взаимной индуктивности между двумя катушками (или собственной индуктивности одной катушки) при внесении в их поле металлического объекта.
Основные ошибки при расчетах и измерениях
Даже при наличии точных приборов и знании формул можно получить некорректный результат из-за неучтенных факторов. Вот наиболее частые ошибки, которых следует избегать.
Рис. 4. Распределение типичных причин ошибок при практическом определении параметров связанных катушек.
- Игнорирование паразитной межвитковой емкости. Любая катушка, помимо индуктивности, обладает и распределенной емкостью между витками. На высоких частотах эта емкость начинает играть заметную роль, образуя с индуктивностью параллельный колебательный контур. В результате измеренное значение индуктивности может сильно отличаться от истинного и будет зависеть от частоты измерения.
- Зависимость параметров сердечника от частоты. Если катушки имеют ферритовый или металлический сердечник, его магнитная проницаемость не является константой. С ростом частоты она уменьшается, а потери в сердечнике растут. Поэтому измерения, проведенные на частоте 1 кГц, могут быть нерелевантны для устройства, работающего на частоте 1 МГц.
- Влияние окружающих предметов. При измерении «воздушных» катушек, особенно с большим полем рассеяния, на результат могут влиять близкорасположенные металлические предметы, включая корпус прибора, инструменты на столе или даже саму печатную плату.
Часто задаваемые вопросы (FAQ)
Рассматривалось только последовательное соединение. а как считать индуктивность двух катушек при параллельном включении?
Да, это важный вопрос. При параллельном соединении двух катушек общая индуктивность также зависит от взаимной индуктивности M. Формула для расчета выглядит так: Lобщ = (L1 * L2 — M²) / (L1 + L2 ± 2M). Знак «плюс» в знаменателе используется для встречного включения, а «минус» — для согласного. Обратите внимание, что здесь логика знаков обратна последовательному соединению, что часто вызывает путаницу. Для определения типа включения используется тот же принцип маркировки начал обмоток.
Можно ли рассчитать общую индуктивность для трех и более катушек?
Да, можно, но расчет значительно усложняется. Для системы из N катушек необходимо учитывать взаимную индуктивность между каждой парой катушек. Например, для трех катушек (L1, L2, L3) нужно будет знать три взаимные индуктивности: M12 (между 1 и 2), M13 (между 1 и 3) и M23 (между 2 и 3). Формула для последовательного согласного включения будет выглядеть так: Lобщ = L1 + L2 + L3 + 2(M12 + M13 + M23). Знак перед M будет зависеть от взаимной полярности включения каждой пары.
Влияет ли толщина провода на индуктивность катушки?
На саму величину индуктивности, которая в первую очередь зависит от числа витков, диаметра и длины намотки, толщина провода влияет незначительно. Однако она оказывает огромное влияние на другой важный параметр — добротность (Q-фактор) катушки. Провод большего сечения имеет меньшее активное сопротивление, что снижает омические потери и, соответственно, повышает добротность. Также толщина провода определяет максимальный ток, который может пропускать катушка без перегрева.
Почему мой LCR-метр показывает разные значения индуктивности на разных частотах?
Это нормальное явление, особенно для катушек с сердечником и на высоких частотах. Существует несколько причин. Во-первых, это собственная паразитная емкость катушки, которая на некоторой частоте (частоте собственного резонанса) входит в резонанс с индуктивностью, что резко искажает показания. Во-вторых, для катушек с ферромагнитным сердечником магнитная проницаемость материала сердечника может уменьшаться с ростом частоты, что приводит к снижению индуктивности. Всегда проводите измерения на частоте, близкой к рабочей частоте устройства, где будет использоваться катушка.
Как определить начало и конец обмоток у трансформатора без маркировки?
Существует простой и безопасный метод. Подайте на первичную обмотку небольшое переменное напряжение (например, 1-2 Вольта от отдельного трансформатора). Соедините один вывод первичной обмотки с одним выводом вторичной. Теперь измерьте вольтметром переменного тока напряжение между двумя оставшимися свободными выводами. Если измеренное напряжение равно сумме напряжений на обмотках (U1 + U2), то вы соединили конец первой обмотки с началом второй (согласное включение). Если напряжение равно разности ( |
U1 — U2| ), то вы соединили конец первой обмотки с концом второй (встречное включение). Таким образом можно однозначно определить фазировку обмоток.
Заключение
Расчет индуктивности двух магнитно-связанных катушек — задача, требующая комплексного подхода, но вполне доступная для освоения. Мы подробно разобрали теоретические основы взаимной индукции, рассмотрели практические методы измерений и факторы, влияющие на результат. Понимание принципов согласного и встречного включения является ключом к точному анализу и проектированию множества электронных схем.
Не бойтесь экспериментировать: вооружившись мультиметром или LCR-метром и полученными знаниями, вы сможете самостоятельно определять все необходимые параметры для ваших проектов. Практика — лучший учитель. Начните с простых катушек, и очень скоро расчеты связанных индуктивностей станут для вас понятной и рутинной задачей, открывая новые горизонты в мире электроники.

 Испытание строительных материалов: зачем и как проверяют надежность на практике
Испытание строительных материалов: зачем и как проверяют надежность на практике  Новостройки в ЗАО Москвы: как выбрать свое идеальное жилье в западном округе
Новостройки в ЗАО Москвы: как выбрать свое идеальное жилье в западном округе  Как создать эффективный и уютный дизайн интерьера медицинской клиники: практические советы и идеи
Как создать эффективный и уютный дизайн интерьера медицинской клиники: практические советы и идеи  Декоративные блюда: Искусство и Функциональность на Вашем Столе
Декоративные блюда: Искусство и Функциональность на Вашем Столе  Зимние шипованные шины Continental: почему они — ваш надежный спутник в холодное время года
Зимние шипованные шины Continental: почему они — ваш надежный спутник в холодное время года  Письменные столы из массива дерева: сочетание стиля, практичности и долговечности
Письменные столы из массива дерева: сочетание стиля, практичности и долговечности  Как правильно выбрать пол в квартиру?
Как правильно выбрать пол в квартиру?  Как выбрать и купить термоконтейнеры: простой гид для каждого
Как выбрать и купить термоконтейнеры: простой гид для каждого  Как набрать больше участников на ваш Discord-сервер
Как набрать больше участников на ваш Discord-сервер  Как подать заявку на регистрацию товарного знака: полное руководство для бизнеса
Как подать заявку на регистрацию товарного знака: полное руководство для бизнеса